AI/ML has become a powerful tool for scientific computation, allowing the community to understand and make new connection in high-dimensional and non-linear systems with complex parameter landscapes. At SCOREC, we innovate both in machine learning techniques and in their application to a wide variety of problems.
Primary Contacts: Max Bloomfield, Shaowu Pan
SCOREC Researchers: Bloomfield, Merson, Pan, Sahni
ML/AI in Scientific Computation Developments
In addition to being a user of machine learning and artificial intelligence methods, SCOREC works to push AI/ML technology forward, developing new techniques, supporting algorithms, and modalities of connecting AI/ML to real-world problems.
Among the specific application developments from SCOREC researchers are:
- Connecting Bayesian dropout approximation to manufacturing process modules.
- LSTM- and GRU-based data reconstruction for computational adaptivity and solution analysis.
- Sophisticated dimensionality reduction of PDE behavior, creating surrogate models completely removed from the underlying mesh.
- Neural network models for upscaling multiscale methods, enforcing physics-based constraints.
- AI agents for guiding model modification and sophisticated meshing.
- Physics-Informed ML for plasma physics.
- Determination of material properties.
- Physics feature detection in large scale simulations.
Robust detection and detection and resolution of solution features
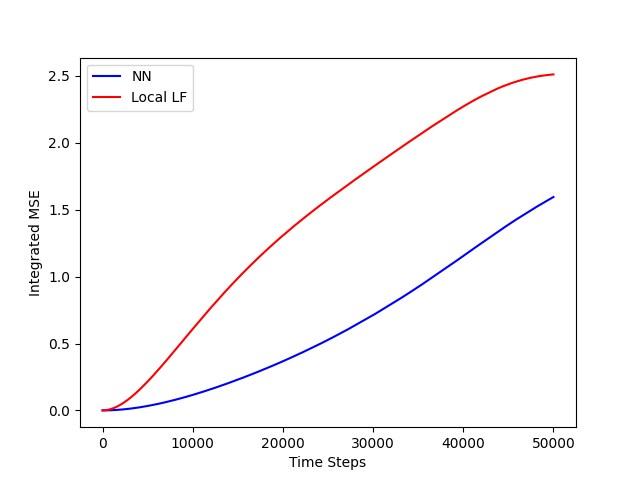
Physics-based feature detection procedures on numerically computed data are often noisy, especially for complex problems with interacting and evolving features (such as shocks). This problem is exacerbated on coarse initial unstructured meshes. Using AI/ML techniques, we have developed an efficient approach to detect and process complex features including those computed on relatively coarse unstructured meshes. We have pioneered using long short-term memory (LSTM) and gated recurrent unit (GRU) based recurrent neural network architectures to augment the ordered sequence of (noisy) data obtained from a physics-based sensor/detector by filling in the missing/fragmented data. The resulting information can be used for feature-based anisotropic meshing, and/or quantitative analysis of complex features including their parametrization and classification.
LSTM-assisted shock detection and processing for a hypersonic case
LSTM-based neural network is employed on the solution computed on a very coarse initial mesh to perform shock detection and processing
LSTM-based neural network is employed on the solution computed on a very coarse initial mesh to perform shock detection and processing
Resulting data is used to automatically construct a shock-fitted mesh
Zoomed view
Reinforcement Learning for Hex Meshing
Hexahedral (hex) meshes are the preferred element technologies for many mesh based PDE simulation coded. Unlike the case of all tetrahedral meshes, fully automatic hex mesh generation methods that yield well controlled meshes over complex geometries are not current available. Reinforcement learning methods are being developed to decompose complex geometric domain into subdomains that can be automatically meshed with well controlled hex meshes.
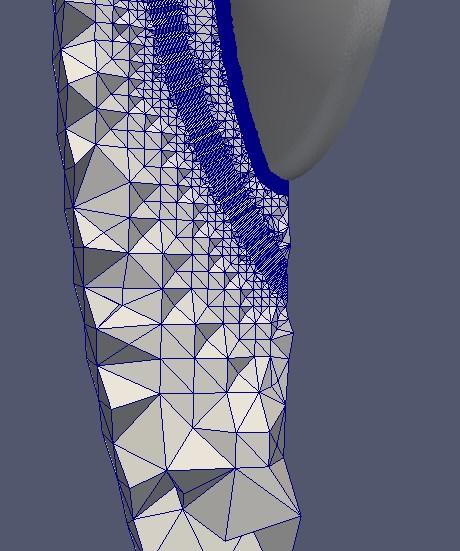
Example of ML driven hex meshing
Original retainer model
Model sectioned by RL agent
Sectioned model meshed to 218k elements
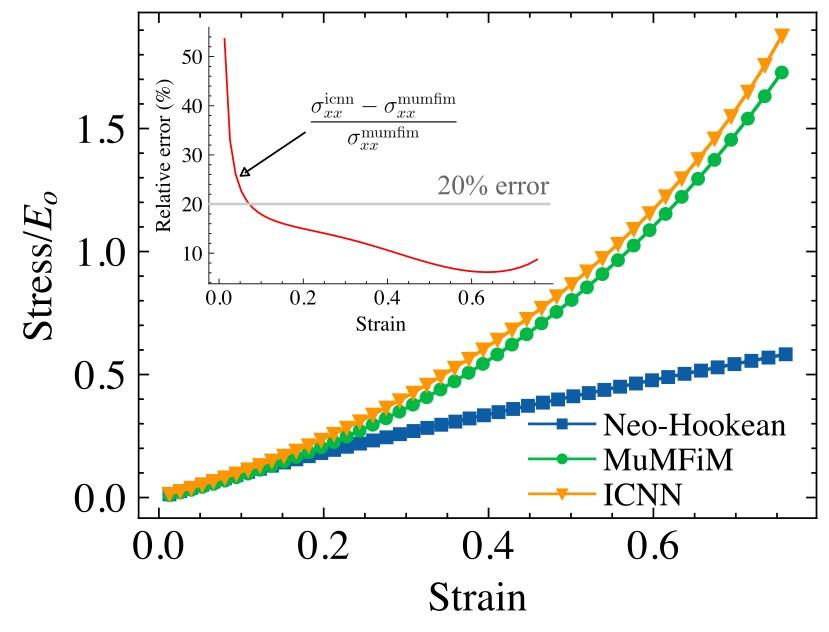
Machine Learned Constitutive Models for Upscaling Multiscale Methods
Constitutive models have strict physical laws that govern their validity. If these are violated, many of the guarantees of solvability no longer hold. The ability of finite elements and other discretization methods to converge relies on these capabilities. We develop neural networks that strictly enforce physical constraints such as polyconvexity and frame-indifference.
ICNN neural network architecture for computing constitutive models
Comparison of stress strain curves with ICNN neural network, Neohookean, and multiscale material models.
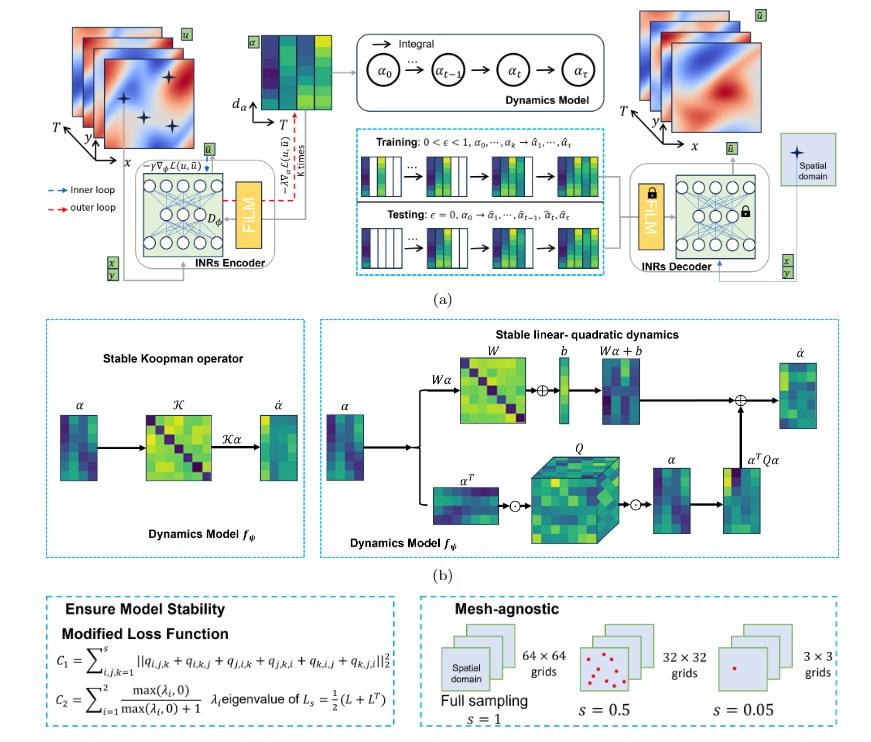
Professor Pan’s group is developing a wide range of AI/ML techniques addressing a wid range of simulation needs including:
Advanced mesh-agnostic surrogate modeling for nonlinear PDE systems
Stability-preserving mesh-agnostic surrogate models for general time-dependent PDEs .
Parametric surrogate models for 3D transonic wing under unseen Mach number, Reynolds number, and angle of attack.
Reference:
[1] Pan, S., Brunton, S.L. and Kutz, J.N., 2023. Neural implicit flow: a mesh-agnostic dimensionality reduction paradigm of spatio-temporal data. Journal of Machine Learning Research, 24(41), pp.1-60.
[2] Pan, S., Implicit neural representations meets interpretable parameterized reduced-order modeling. In 2024 Fall Eastern Sectional Meeting. AMS.
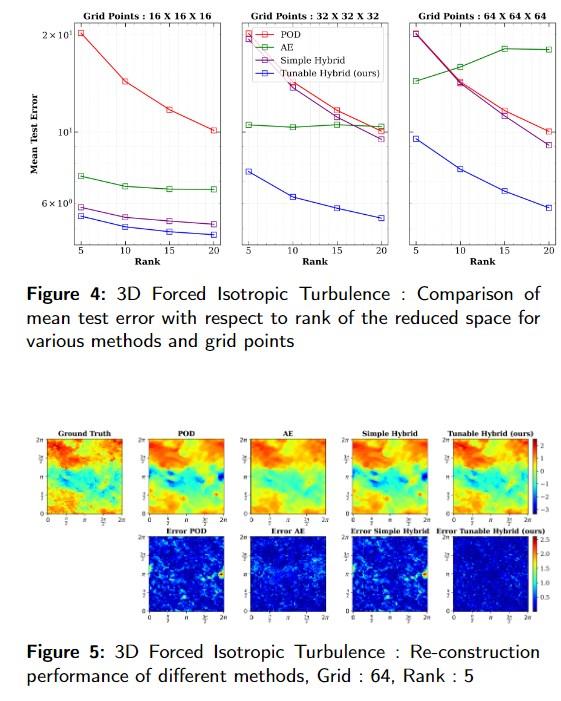
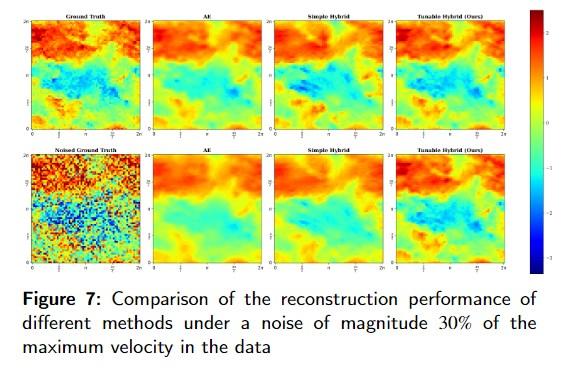
Representation learning of turbulent flows
Hybrid SVD-DNN framework captures finer details of 3D turbulence compared to the state-of-the-art deep learning frameworks.
Reference:
[1] Somasekharan, N. and Pan, S., 2024. Hybrid Auto-Encoder with SVD-like Convergence. Bulletin of the American Physical Society.
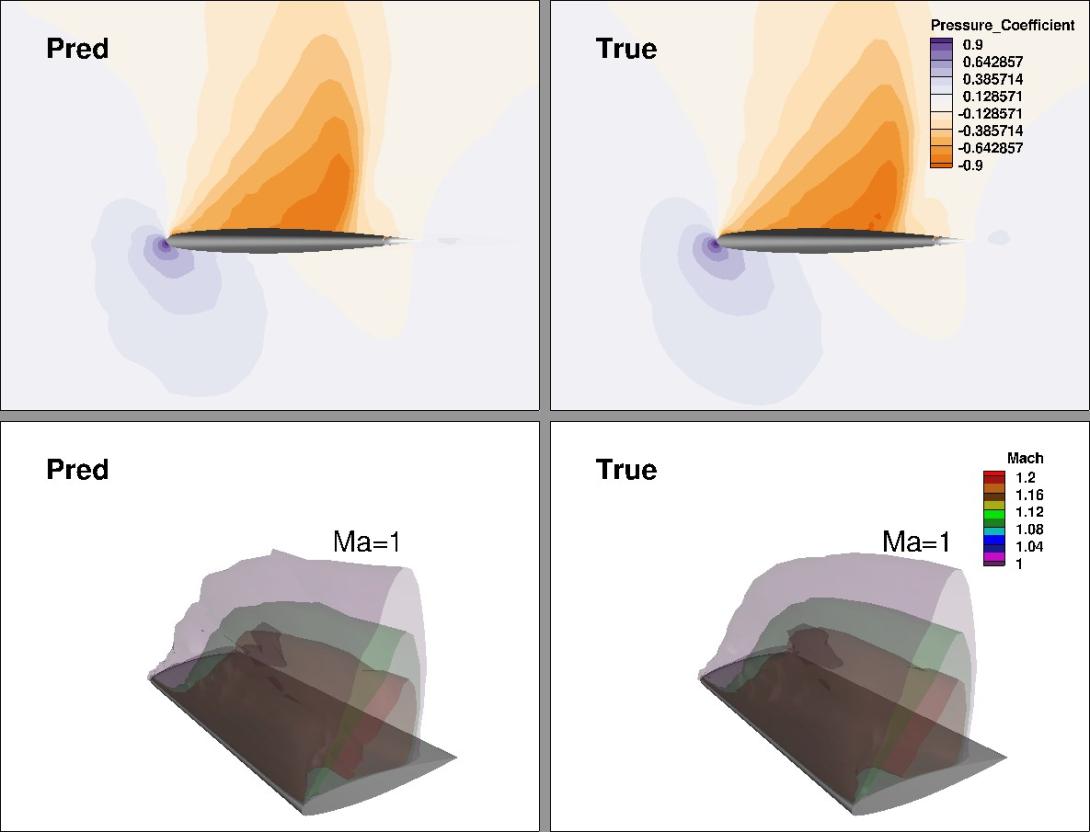
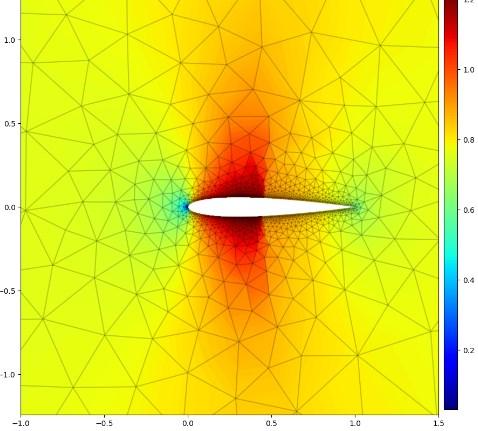
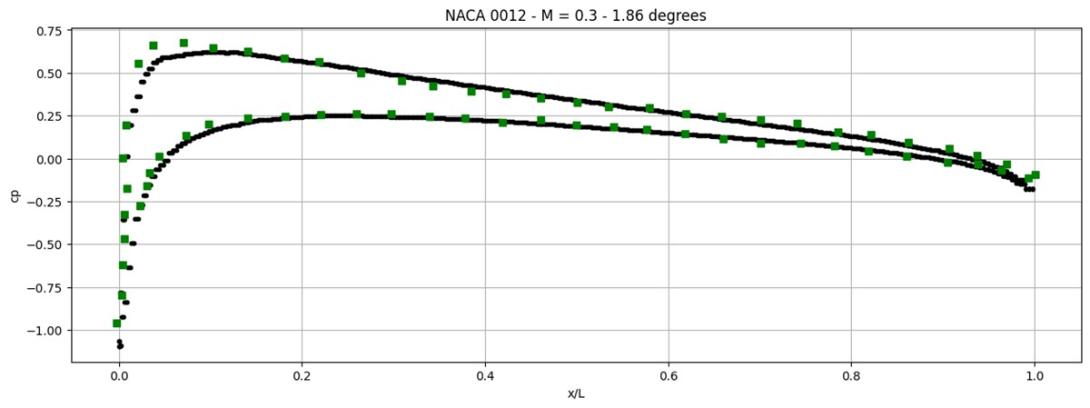
Neural Finite Element Method for Compressible
Framework provides a seamless ML-FEM computational platform on GPU for developing new physics-informed learning algorithms. On the right is an example of solving 2D inviscid transonic flow over a NACA0012 airfoil with discontinuous Galerkin Method.
Reference:
[1] Somasekharan, N. and Pan, S., 2023. Warp-DG: A Differentiable Discontinuous Galerkin Solver for Compressible Flows. Bulletin of the American Physical Society.
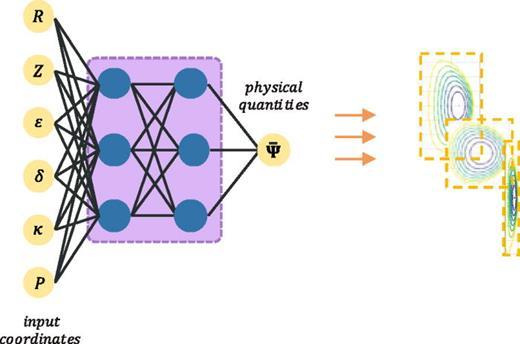
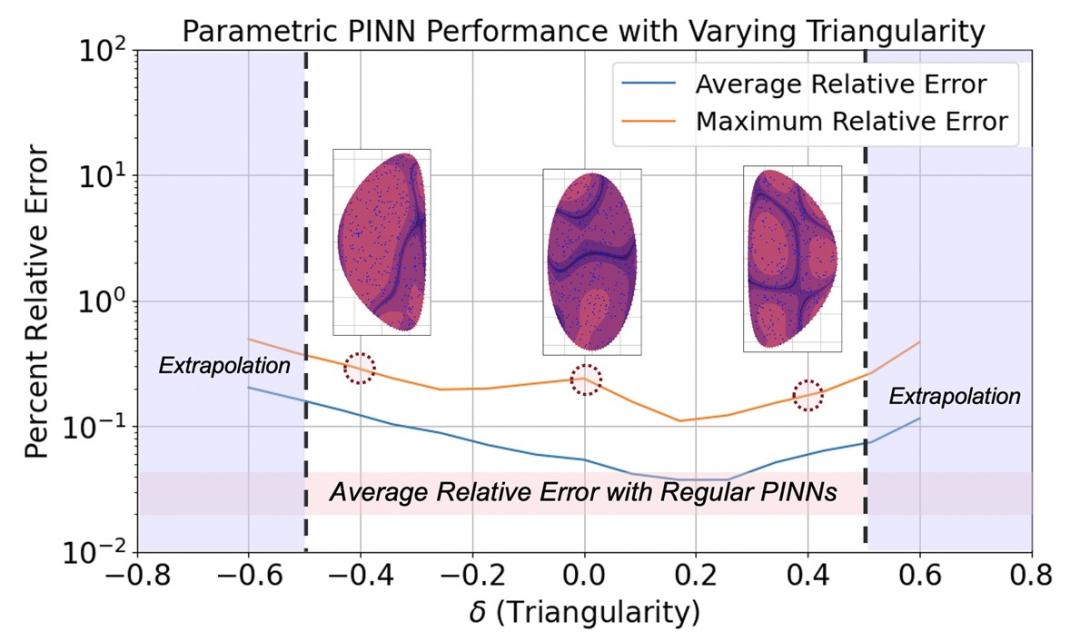
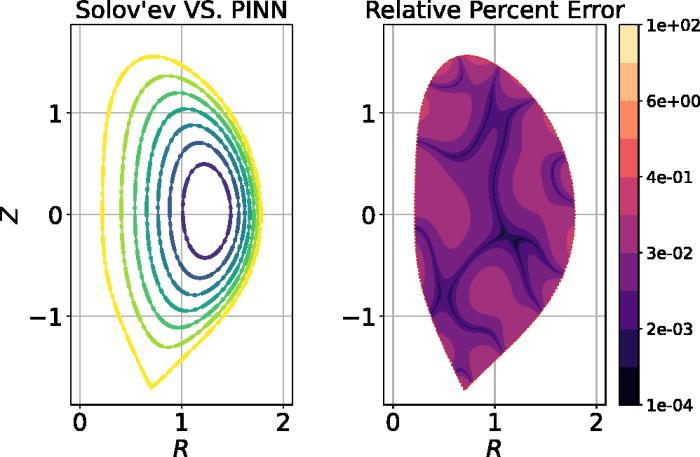
Physics-Informed Machine Learning for Plasma Physics
Deep neural networks are utilized to parameterize the solution of Grad-Shafranov equilibria while ensuring compliance with conservation laws. Once trained, the model can accurately solve any GS equilibrium within the range of geometric variations covered during training, eliminating the need for meshing and running new simulations.
Error prediction by physics informed neural network
Reference:
[1] Jang, B., Kaptanoglu, A.A., Gaur, R., Pan, S., Landreman, M. and Dorland, W., 2024. Grad–Shafranov equilibria via data-free physics informed neural networks. Physics of Plasmas, 31(3).