The goal of high-fidelity design optimization is to couple accurate simulations, typically based on partial-differential equations (PDEs), with numerical design optimization. The need for high-fidelity models arises for systems governed by complex, nonlinear phenomena; for example, fluid flow over a wing during landing or plasma in a fusion reactor. If a simple model is used in these circumstances, an optimization algorithm may exploit errors and produce invalid designs. The risk of an invalid solution is especially high when an unconventional design leads to extrapolation of a simple model.
The principal challenge of high-fidelity design optimization is the computational expense of the models. The algorithms used to find the optimal design must be very efficient, because we do not have the luxury of endlessly sampling a fast-to-execute analytical model. For this reason, gradient-based methods are typically favored for high-fidelity design optimization, especially when there are many design parameters.
Below we summarize some algorithmic developments within SCOREC that focus of gradient-based, high-fidelity design optimization.
Primary Contact: Jason Hicken
SCOREC Researchers: Hajela, Hicken
Optimization Algorithm Developments
Newton-based Optimization Algorithms
SCOREC research has contributed to Newton-based optimization algorithms that leverage second-derivative information. The benefit of Newton's method is greatly improved algorithmic scaling: Newton's method takes many fewer iterations to find the optimal design compared with first-order and quasi-Newton optimization methods. The disadvantage of Newton's method is that each iteration can be significantly more expensive.
To mitigate this disadvantage, SCOREC researchers have developed state-of-the-art Newton-Krylov optimization algorithms. These algorithms do not require the user to provide second-derivatives explicitly, greatly reducing the implementation burden of Newton's method. The Center has developed Newton-Krylov algorithms for both constrained and unconstrained optimization problems, and we have demonstrated that these algorithms can efficiently solve large-scale problems with thousands of design parameters.
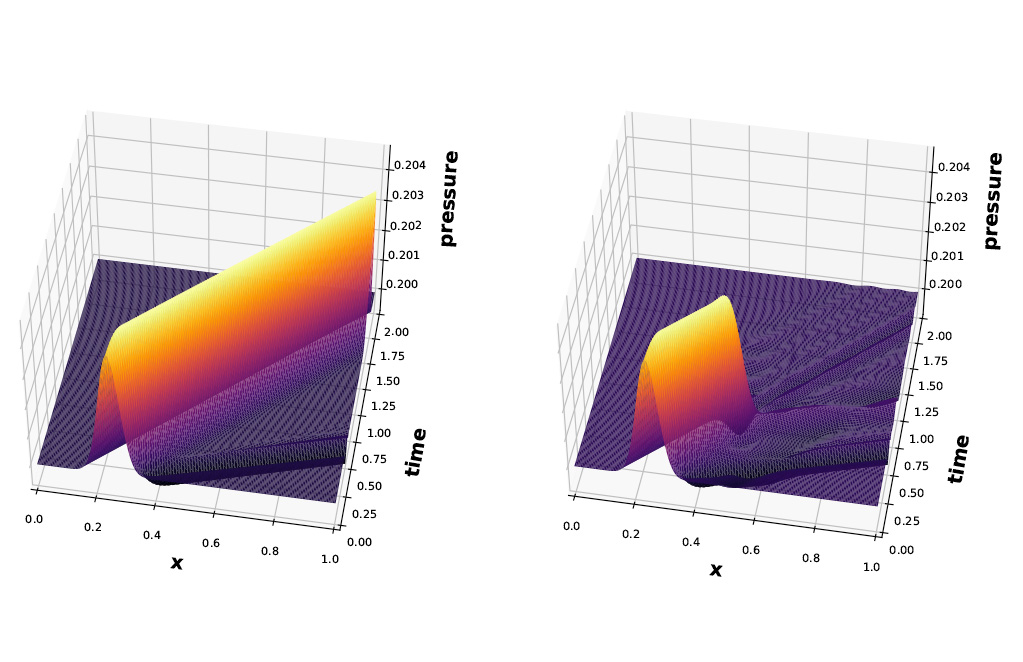
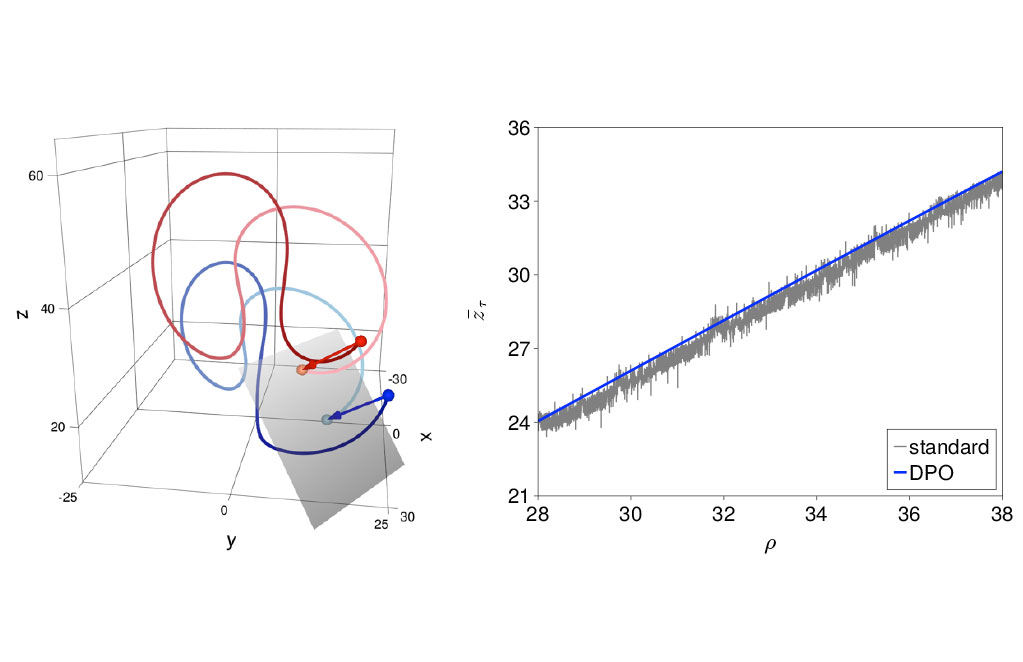
Optimization of Chaotic Systems
Chaotic dynamical systems are ubiquitous in science and engineering, but they present unique challenges in the context of optimization. In particular, time-averaged outputs from a chaotic simulation (e.g. lift on an aircraft) are characterized by high-frequency, noise-like variations in parameter space. These oscillations make conventional gradient-based optimization algorithms ineffective.
SCOREC researchers have developed a method to regularize time-averaged outputs, thereby making them amenable to gradient-based optimization. In short, this algorithm turns initial-value problems into periodic boundary-value problems in time. By tying the final and initial states together, the chaotic “butterfly” effect is suppressed and time-averaged outputs become smooth in parameter space.
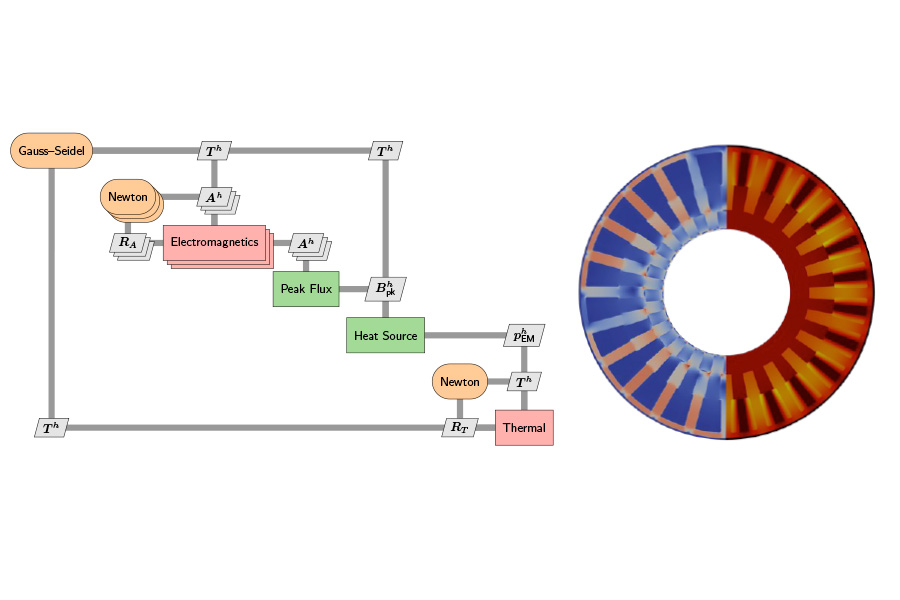
Multidisciplinary Design Optimization
Most systems that are of interest to engineers and scientists are multidisciplinary in nature. For such systems one cannot model one discipline (i.e., structural, fluids, thermal, ...) in isolation and expect reliable predictions. Consider an aircraft's wing during a maneuver. The aerodynamic loads cause the wing's structure to deflect, which changes the shape of the wing, which changes the loads, and so on. When distinct disciplines are coupled tightly, it becomes critical that the coupling is accurately modelled during the optimization process.
Researchers in SCOREC have been active in the field of Multidisciplinary Design Optimization (MDO) for several decades. We have addressed challenges ranging from sensitivity analysis of MDO systems (i.e., computing gradients efficiently) to optimization algorithms and MDO architectures. Our recent efforts have focused on Newton-Krylov algorithms for MDO, and the electro-thermal optimization of aircraft electric motors.