Multiscale Computations and Code Coupling | Scientific Computation Research Center

Components of a multiscale simulation capability include:

The ability to solve the models at each of the scales under consideration.
Robust methods to bridge the scales of interest.
The ability to combine the individual model solution methods with appropriate coupling strategies to create a coherent multiscale simulation capability.
Ongoing efforts are addressing the need to match the coupling method with the levels of scale separation for the cases under consideration and to address the need to effectively couple existing single scale models to create coupled multiscale simulations.

Primary Contact: Jacob Merson

SCOREC Researchers: Bloomfield, Merson, Picu, Sahni, Shephard, Smith

Multiscale Computations Developments

Scale coupling technologies must be properly matched to the length and time scales of models being coupled and degree of scale separation. There are two broad classes of scale coupling methods being developed. The first is upscaling (traditionally called hierarchical) which can be used when there is large scale separation between macro and microscales and can use either the same or different physical models on each scale. Examples of this are the variational multiscale method and first order homogenization. The second category of multiscale methods is resolved-scale methods (traditionally called concurrent methods) that contain separate physical models that share the same length scale. Examples of this include the atomistic to continuum coupling (and core-edge coupling of fusion plasmas.

SCOREC research emphasizes capabilities that can bring multiscale simulation techniques to bear on large scale engineering problems using high-performance and GPU accelerated computing.

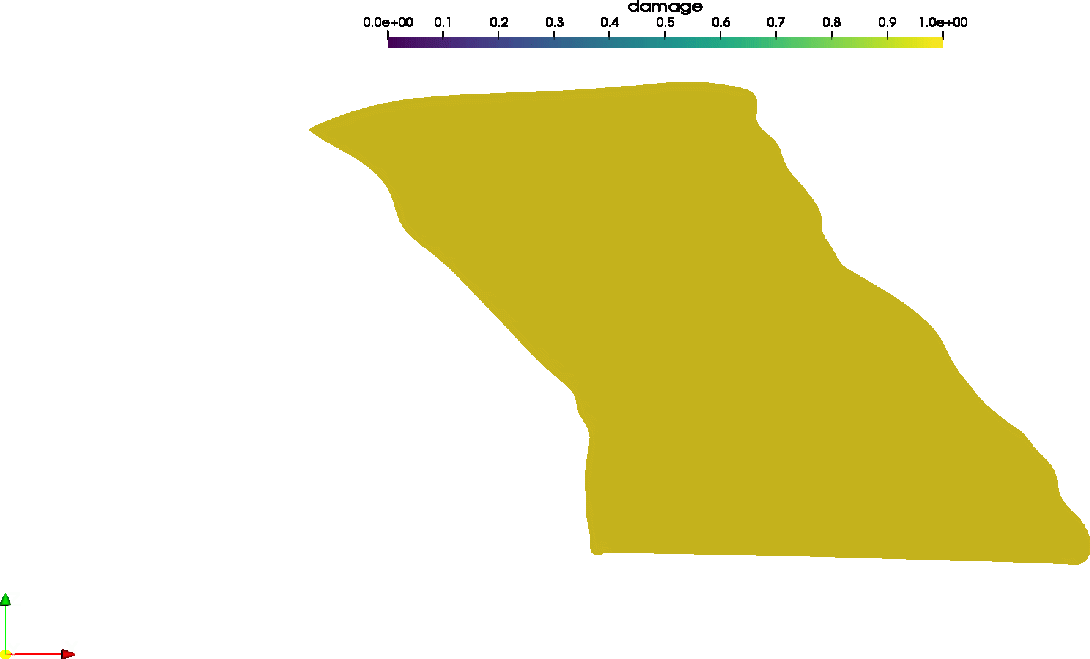
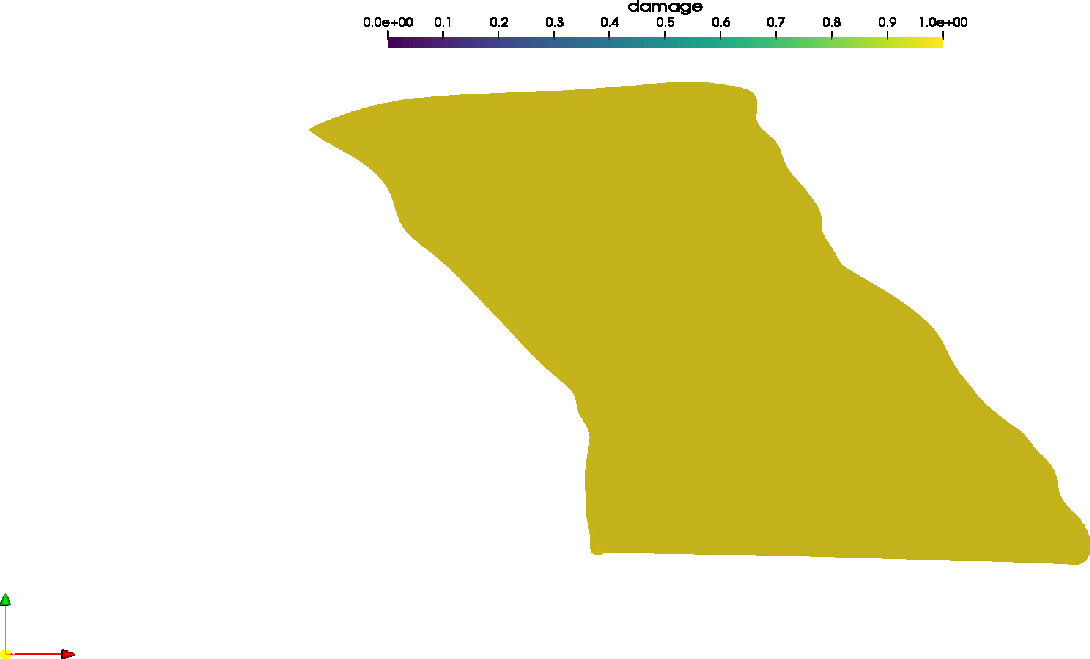
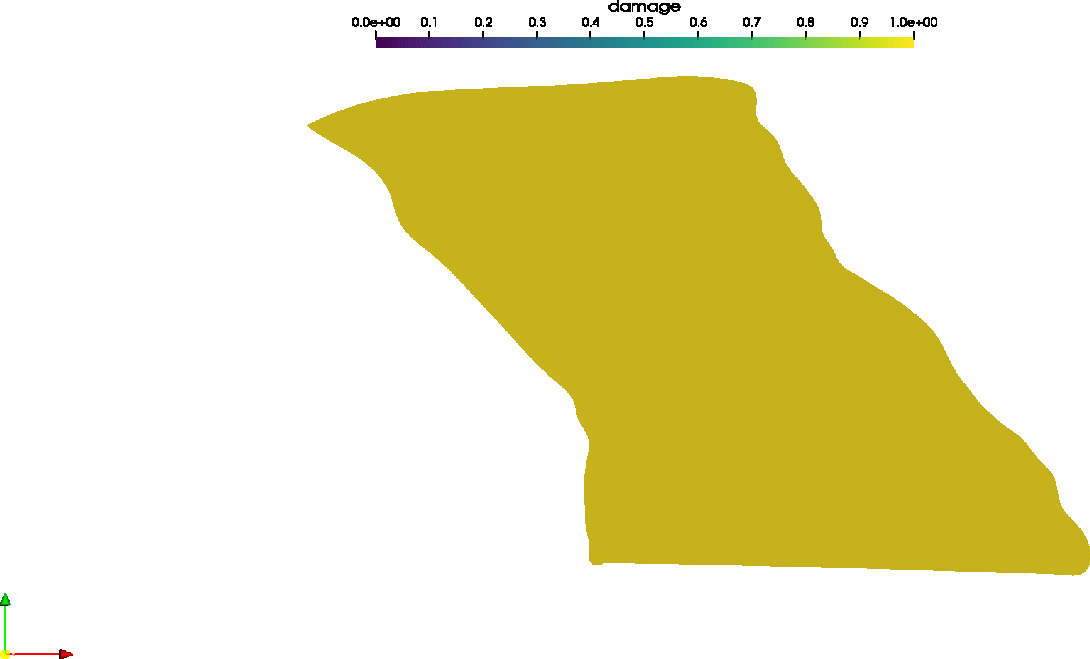
Upscaling multiscale methods are deployed to address fundamental questions in the behavior of fibrous biological materials. Traditional constitutive modeling techniques are not able to capture the range of nonaffine and non-local response that these materials exhibit. The MuMFiM multiscale simulation code has been GPU accelerated and used to analyze biological structures such as damage in the Facet Capsular Ligament (featured below).

Key Software: https://github.com/SCOREC/mumfim

Damage field in the Facet Capsular Ligament

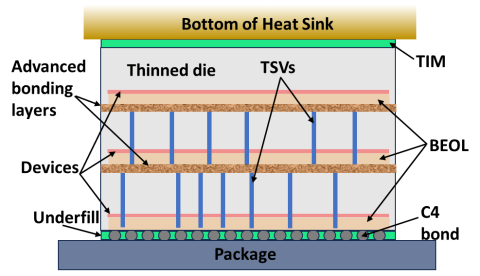
Example of hierarchical multiscale method used for microelectronic chip stacks.

MuMFiM has been extended to address thermal simulations to accelerate the engineering design process for heterogeneously integrated and 3D microelectronic devices. In these devices, the relevant length scales span more than 9 orders of magnitude. The upscaling method in MuMFiM is employed to determine how having the BEOL in the heat path will impact hot spot creation.

VMS-based error estimation and mesh adaptation for precursor shocks due to firing of a projectile from a cannon

The variational multiscale (VMS) method has been used to develop finite element formulations for advection-dominated problems. In the VMS method, a projection is carried out to achieve a scale decomposition or separation. Such a scale separation has been used to model the subgrid-scale stresses in a turbulent flow to perform large-eddy simulations (LES) for complex-geometry problems involving unstructured meshes. This has been combined with a local form of the variational Germano identity to dynamically compute the unknown model parameters (e.g., eddy-viscosity) and apply dynamic LES for inhomogeneous turbulent flows. In addition, scale-separation due to the VMS method has been used to develop explicit a-posteriori error estimator and drive mesh adaptation for complex problems including those involving evolving geometries.

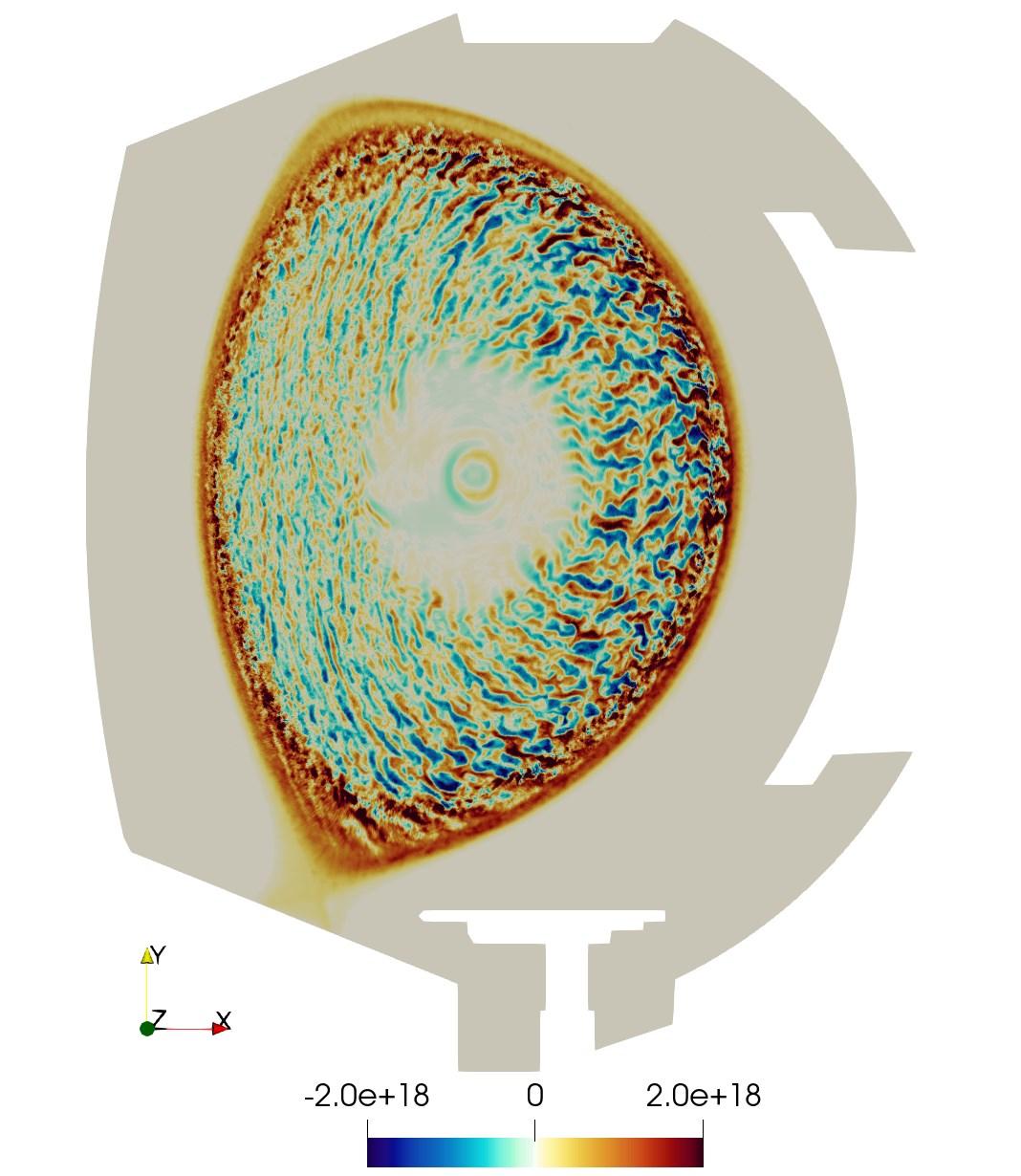
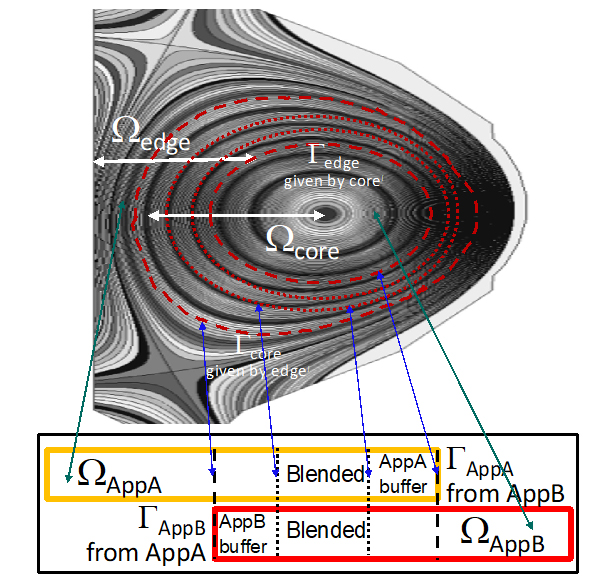
Adaptive refinement in an atomistic-continuum model for the case of a nanoporous crystal.

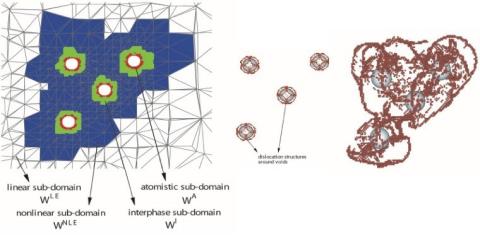
Atomistic simulations fill an important role in their ability to capture microstructural phenomenon like dislocations and crack formation. However, despite advances, atomistic calculations are quite limited in the range of length and timescales they can be used to simulate even on exascale supercomputers. Scale-resolved multiscale methods help bridge this gap, using atomistic simulations where needed, e.g., at crack tips, and continuum finite elements elsewhere. SCOREC researchers have made key contributions to the techniques associated with these methods and can bring them to bear on large scale simulations.

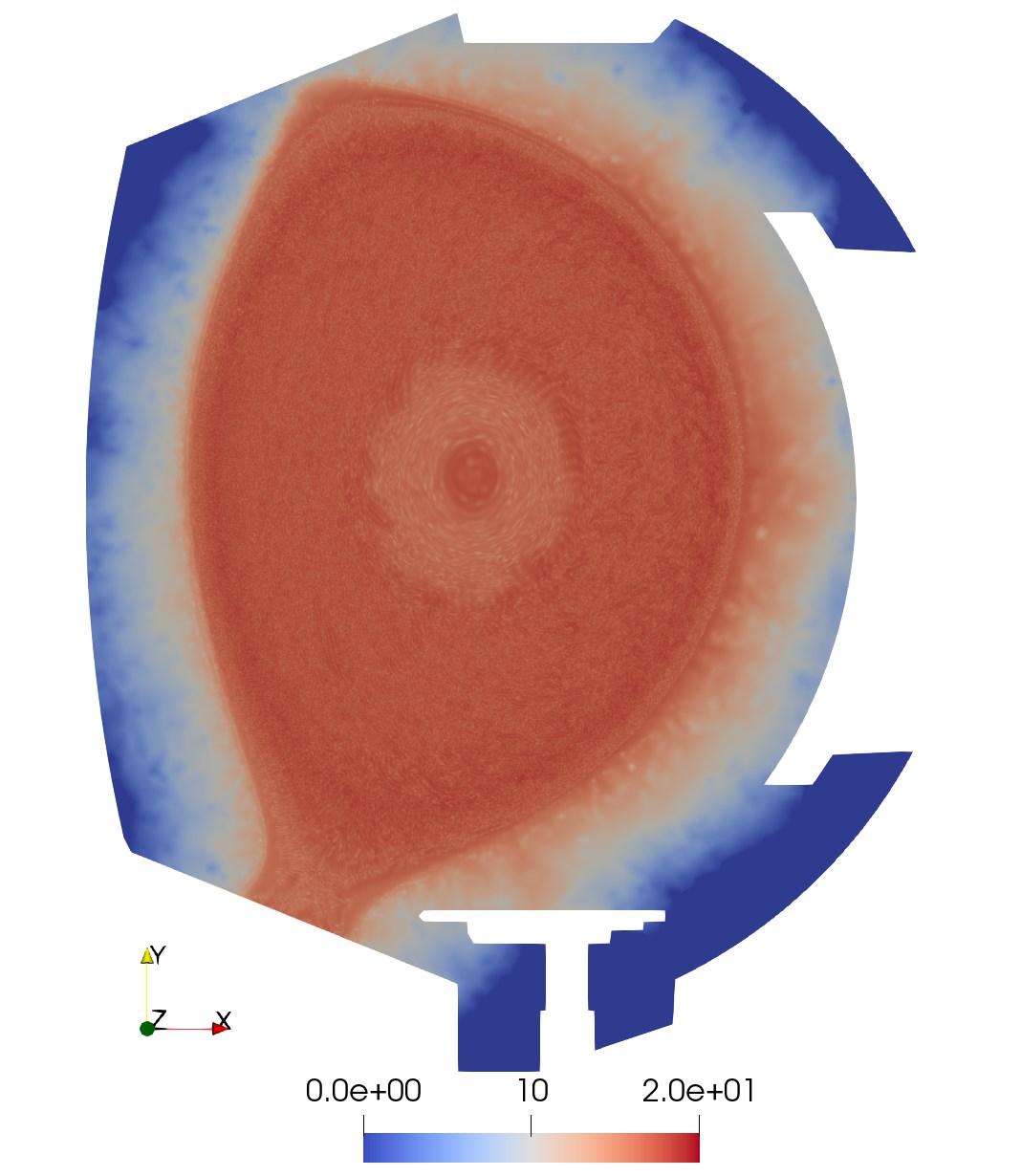
Geometry informed domain decomposition For multiscale simulations The need for scale-resolved multiscale simulations goes well beyond classical mechanics problems such as atomistic-to-continuum methods. They will play a key role in enabling fusion reactor research where a range of physics and engineering simulation methods must be coupled to model a full reactor, or full facility. Building upon developments made during the DOE’s Exascale Computing Project, SCOREC has developed the Parallel Coupler for Multimodel Simulations (PCMS) which provides the building blocks to construct concurrent multiscale simulations with limited impact to the existing analysis codes.

Code Coupling Developments

Optimal performance can be obtained by implementing the individual component simulation code models and coupling procedures within a framework built on a consistent set of data structures and methods. However, in many cases, this is not practical since many thousands of hours have gone into the development of specialized simulation codes and there is no reasonable way to easily fit these codes within a framework without a total rewrite. The Parallel Coupler for Multimodel Simulations (PCMS), currently under development, and applied to specific coupling activities, takes an alternative approach to avoid modification of existing data structures and algorithms. Key PCMS features:

Couple existing simulation codes without requiring component code modification.
Consistent and accurate coupling of models and fields.
Structures and functions to support coupling operations including scale bridging.
Effective coordination of parallel execution on systems from workstations to exascale computers employing a rendezvous method.
Accounting for complex coordinate and data transformations.
Effective data transfer using file based and/or in-memory coupling build on Adios2.

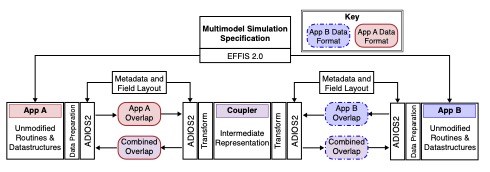
Diagram of the Parallel Coupler for Multimodel Simulation components

Effectively coupling of analysis codes requires high quality field transfer operations that can conserve physical quantities. Fusion applications utilize a wide range of coordinate systems and have specialized physical constraints that field transfer methodologies must be cognizant of. PCMS contains a range of field transfer methods that support higher dimensional phase space and complex coordinate systems. The design of PCMS is intended to enable experimenting with different field transfer methods to find one that effectively supports the applications needs. In the figures below, we show an example of performing 10 iterations of field transfer between cell centered and nodal data of the ion density field that has been simulated using XGCm.

Example of mapping ion density field mappingusing radial basis functions.

XGC mesh with 611,359 elements and 306, 002 nodes

𝑖𝑑𝑒𝑛𝑠𝑖𝑡𝑦 loaded as the exact/initial field in the coupler app

𝑖𝑑𝑒𝑛𝑠𝑖𝑡𝑦 after 10 MLS-RBF interpolation operation

𝑖𝑑𝑒𝑛𝑠𝑖𝑡𝑦 error field after 10 MLS-RBF interpolation operation

Key Publications:

D. E. Keyes et al., “Multiphysics simulations: Challenges and opportunities,” The International Journal of High Performance Computing Applications, vol. 27, no. 1, pp. 4–83, Feb. 2013, doi: 10.1177/1094342012468181.
J. Fish et al., “concurrent AtC coupling based on a blend of the continuum stress and the atomistic force,” Computer Methods in Applied Mechanics and Engineering, vol. 196, no. 45–48, pp. 4548–4560, Sep. 2007, doi: 10.1016/j.cma.2007.05.020.
M. A. Nuggehally, M. S. Shephard, R. C. Picu, and J. Fish, “Adaptive Model Selection Procedure for Concurrent Multiscale Problems,” Int J Mult Comp Eng, vol. 5, no. 5, pp. 369–386, 2007, doi: 10.1615/IntJMultCompEng.v5.i5.20.
P. E. Davis et al., “Benesh: Choreographic Coordination for In-situ Workflows,” presented at the 30th IEEE International Conference on High Performance Computing, Data, and Analytics (HiPC), Goa, India, Dec. 2023. doi: 10.1109/HiPC58850.2023.00047.
M. S. Shephard et al., “Unstructured mesh tools for magnetically confined fusion system simulations,” Engineering with Computers, vol. 40, no. 5, pp. 3319–3336, Oct. 2024, doi: 10.1007/s00366-024-01976-2.
J. S. Merson, C. R. Picu, and M. S. Shephard, “A new open-source framework for multiscale modeling of fibrous materials on heterogeneous supercomputers,” Engineering with Computers, pp. 1–19, 2024, doi: 10.1007/s00366-023-01934-4.
N. Parvez and J. Merson, “A physics preserving neural network based approach for constitutive modeling of isotropic fibrous materials,” Engineering with Computers, Dec. 2024, doi: 10.1007/s00366-024-02095-8.