The development of new discretization methods continues to be a major area of research driven by several factors. Specific classes of PDE, like those with multiscale nature for problems dealing with plasma and turbulence, continue to be challenging to discretize effectively. Similarly, multiphysics, multidomain and multimaterial problems, such as those with evolving interfaces and chemical reactions, require new developments to ensure stability and accuracy. Our developments span a wide range of numerical methods accounting for sub-grid scale effects, anisotropy, discontinuities, energy- and entropy-stability, immersed techniques and stable multi-domain partitioned algorithms. Furthermore, to enhance the accuracy of the numerical solution, adaptive mesh control methods are designed to match the needs of the discretization technologies being employed. In addition, these methods are deployed to most effectively use today’s accelerator-based parallel computers. PDE discretization technologies being investigated include overset grid methods, adaptive variational multiscale, summation by parts, immersed finite element methods, fluid structure interaction by added mass partitioning.
Primary Contact: Onkar Sahni
SCOREC Researchers: Banks, Henshaw, Hicken, Li, Maniatty, Sahni, Shephard, Tumuklu, Zhang
Overset Grid Methods
Overset grid methods have been used to develop efficient and high-order accurate finite difference and finite volume methods for problems in complex geometry. They are especially useful for problems with moving and deforming boundaries and interfaces. See overtureFramework.org for more information and a list of publications.
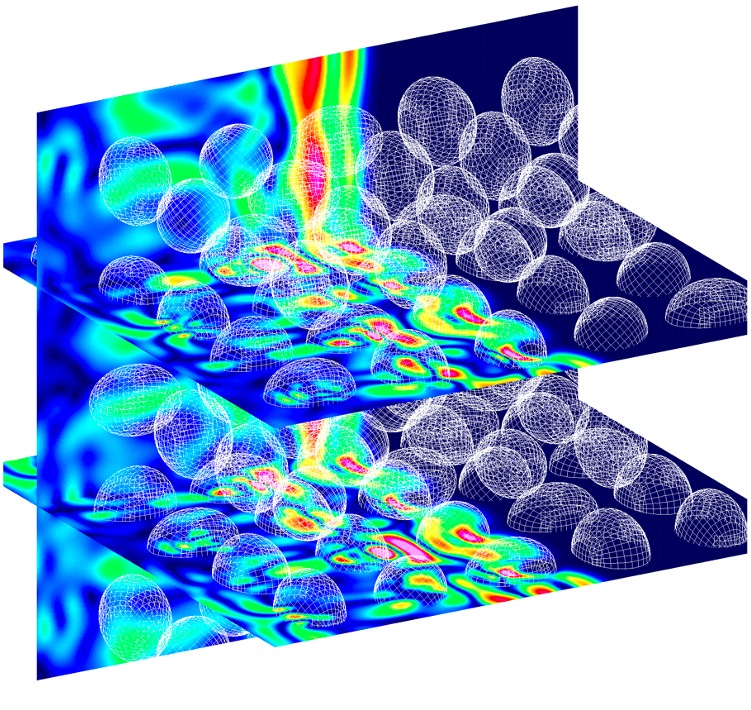
Adaptive Variational Multiscale Methods
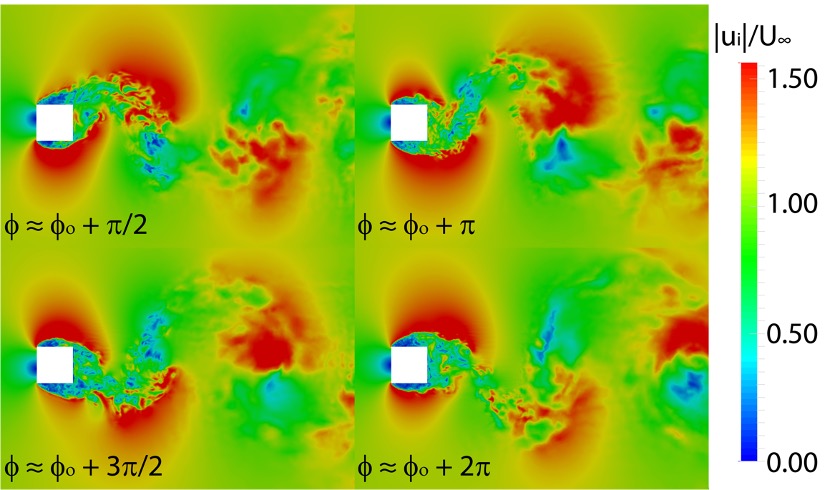
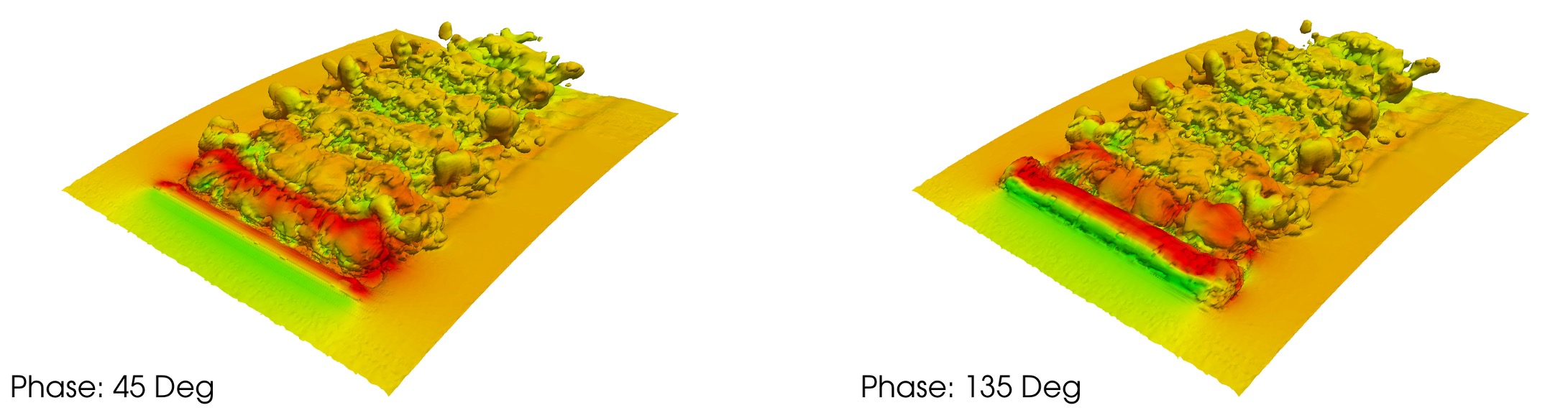
The variational multiscale (VMS) method has been used to develop finite element formulations for advection-dominated problems. In the VMS method, a projection is carried out to achieve a scale decomposition or separation. Such a scale separation has been used to model the subgrid-scale stresses in a turbulent flow to perform large-eddy simulations (LES) for complex-geometry problems involving unstructured meshes. This has been combined with a local form of the variational Germano identity to dynamically compute the unknown model parameters (e.g., eddy-viscosity) and apply dynamic LES for inhomogeneous turbulent flows. In addition, scale-separation due to the VMS method has been used to develop an explicit a-posteriori error estimator and drive mesh adaptation for complex problems including those with evolving geometries.
Summation-by-parts Methods
Summation-by-parts (SBP) operators mimic integration by parts at the discrete level; that is, at the level of numerical quadrature. They were originally proposed by Kreiss and Scherer (https://doi.org/10.1016/B978-0-12-208350-1.50012-1) in order to construct stable discretizations of linear hyperbolic partial differential equations.
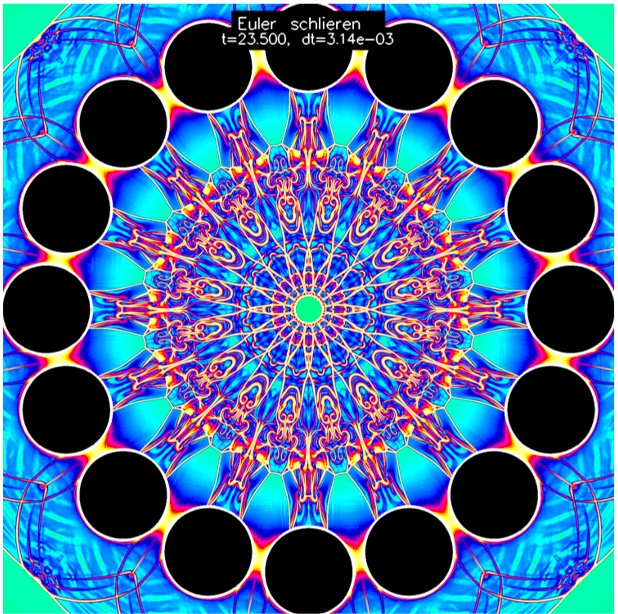
For many years, SBP methods remained somewhat obscure, but interest in these methods grew dramatically when Fisher and Carpenter — see, for example, https://dx.doi.org/10.1016/j.jcp.2013.06.014 — showed that SBP operators could be used to construct high-order, entropy-stable discretizations for hyperbolic conservation laws, such as the Euler equations of gas dynamics. Fisher and Carpenter's work was significant, because the widespread adoption of high-order discretizations for compressible flows has been hindered, in part, by their “fragility” and lack of robustness.
SCOREC researchers have made fundamental contributions to the theory and implementation of SBP methods, which have helped extend these methods beyond conventional, multi-block finite-difference methods. Some of our contributions to the field are summarized below.
- Superconvergence of functionals based on SBP operators (http://dx.doi.org/10.1137/100790987).
- A definition of multi-dimensional SBP operators suitable for triangular and tetrahedral elements (http://dx.doi.org/10.1137/15m1038360) and curved elements (http://dx.doi.org/10.1016/j.jcp.2017.12.015).
- Entropy-stable, discontinuous Galerkin-difference discretizations based on the SBP property (https://doi.org/10.1016/j.cam.2022.114885).
- SBP operators defined on point clouds over complex domains (https://doi.org/10.1016/j.jcp.2025.113940).
Researchers interested in experimenting with multi-dimensional SBP discretizations can take advantage of the Julia package SummationByParts.jl, which is available as a registered package through the Julia package ecosystem.
Immersed Finite Element Methods
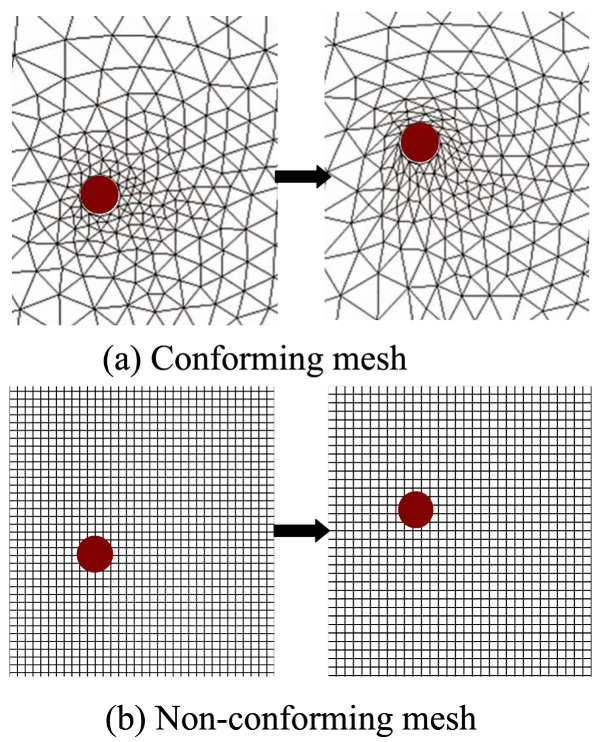
To enable accurate and efficient multiphysics simulations the immersed finite element method (IFEM) has been developed. IFEM is based on the immersed boundary method, in which finite element approaches are used to handle complex fluid–structure interactions and other coupled phenomena without requiring conformal mesh generation. Flexible overlapping domain and interface treatments and robust numerical schemes have been incorporated to improve stability, scalability, and applicability across a wide range of engineering and biomedical problems. To support modular implementation and flexible coupling of multiple physics, the OpenIFEM software (https://github.com/OpenIFEM/OpenIFEM) has been developed and maintained as an open-source platform. OpenIFEM is distributed under the Apache 2.0 License and uses CMake to configure and build based on user-specified applications, which further provides flexibility and ease of deployment.
Partitioned Methods for Fluid Structure Interaction (FSI)
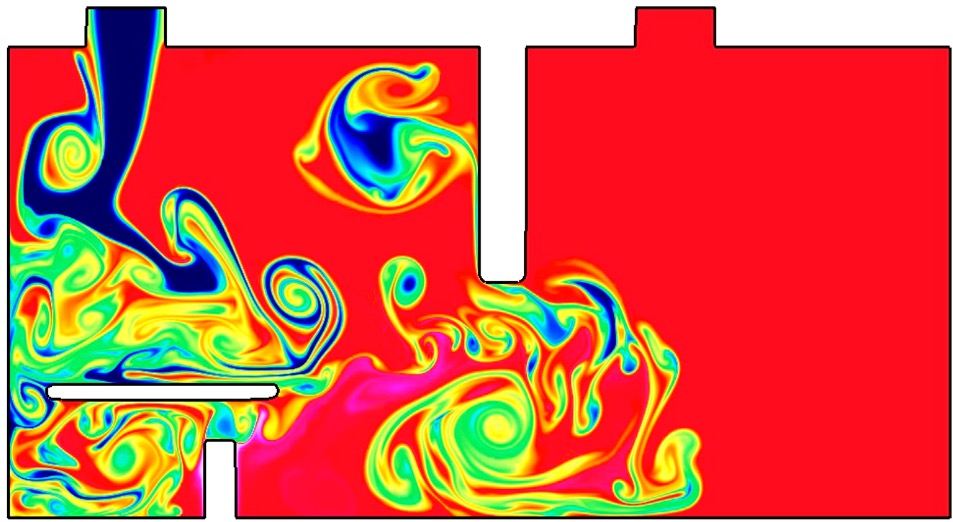
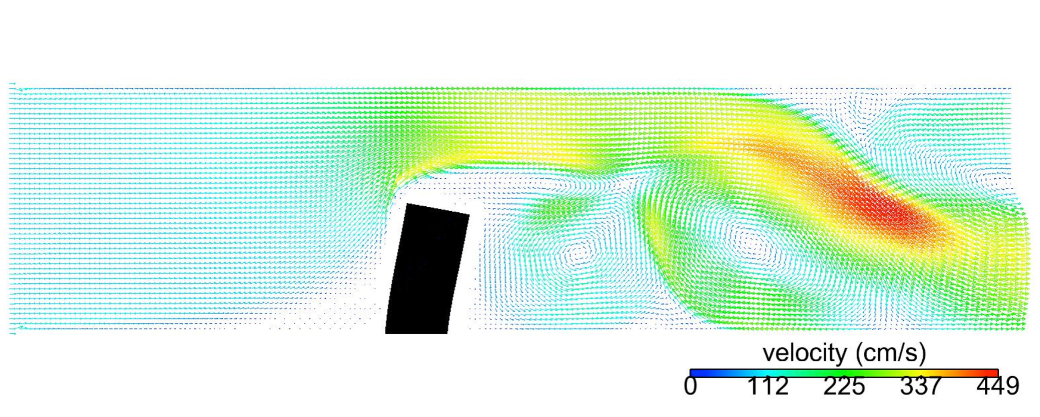
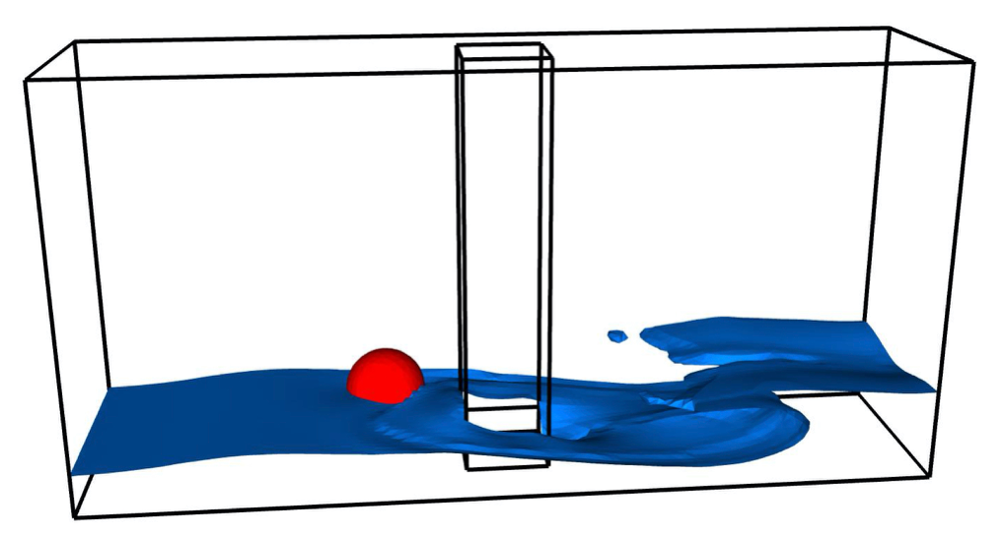
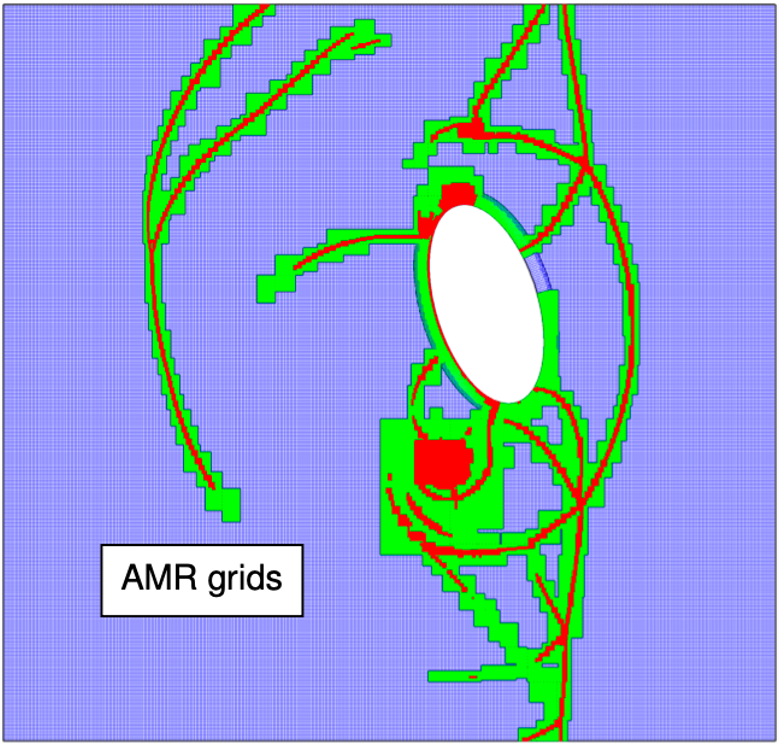
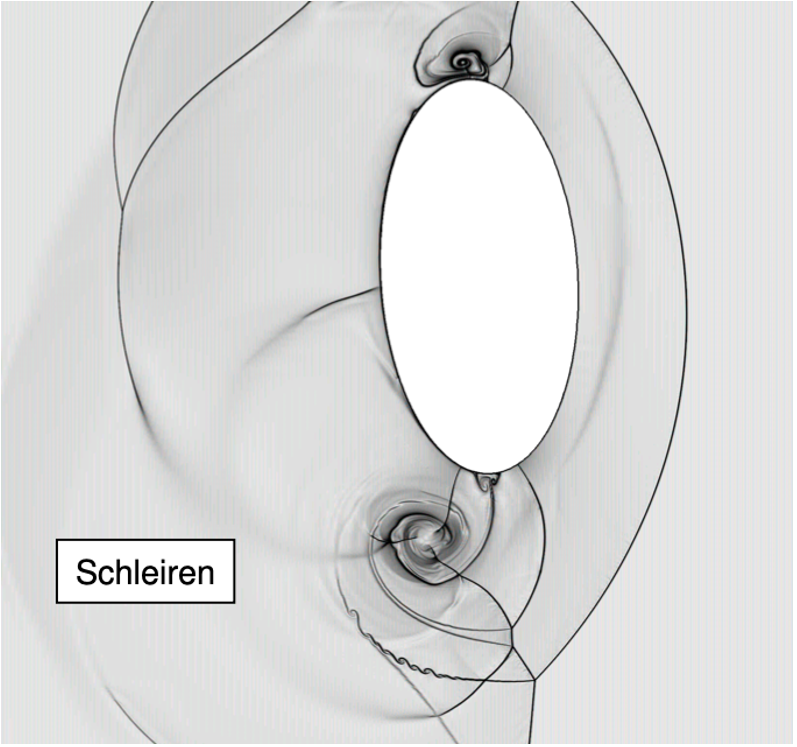
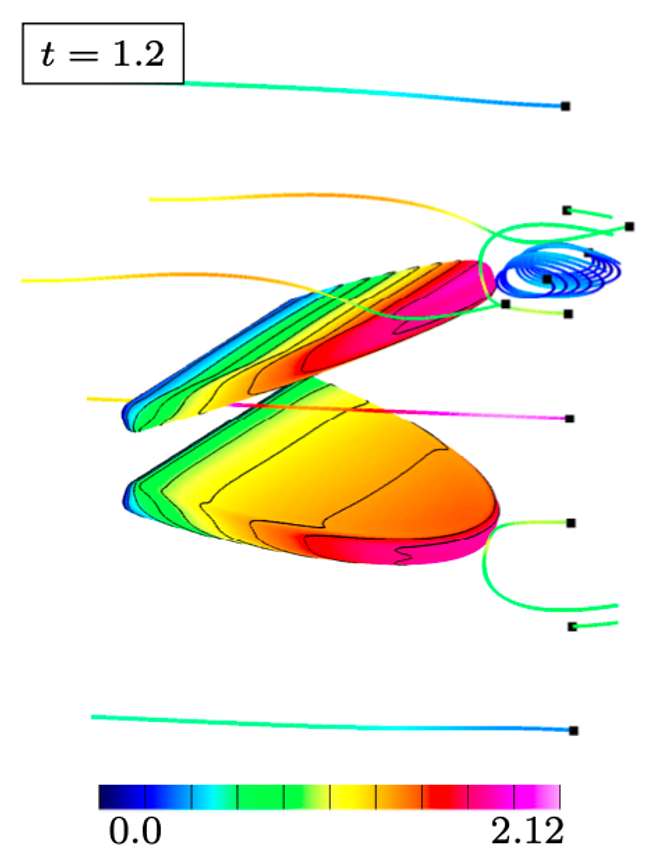
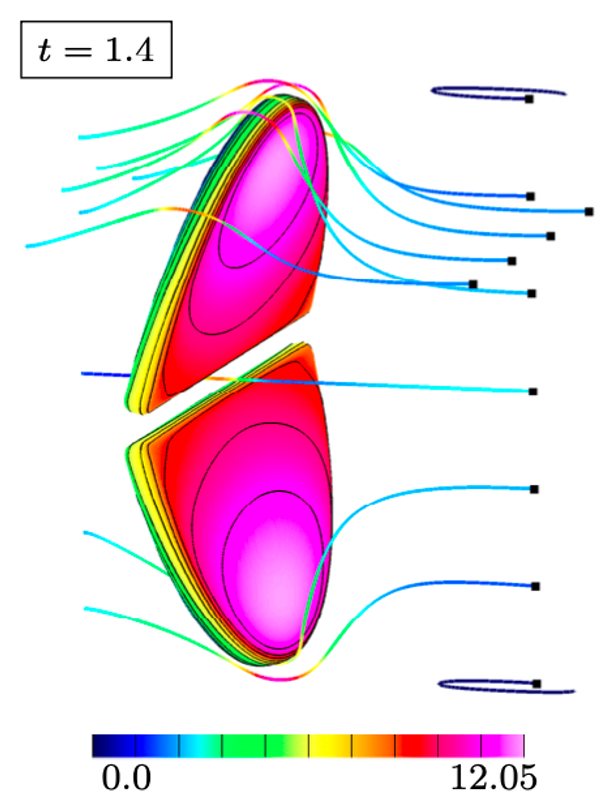
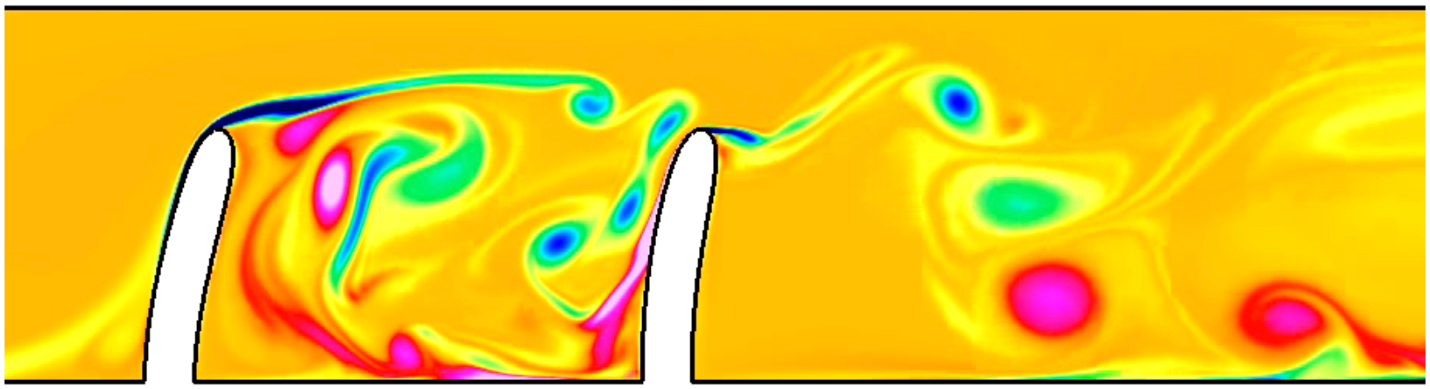
FSI, a particular instance of coupled multi-physics systems, is commonly encountered in many fields of science and engineering, and has many important applications such as wind power, blast-structure interaction, biological flows, and micro-fluidic devices. Traditional partitioned FSI schemes do not take into account the strong coupling between the fluid and solid, and can therefore exhibit an instability whereby an over-reaction of a light solid to an applied force from the fluid leads in turn to an even larger reaction from the fluid and so on. The focus of our work has been addressing these difficulties, and we have shown the construction of stable and accurate algorithms that overcome the added-mass instability for a variety of FSI regimes including those with both compressible and incompressible flows. The essence of the work is to use detailed analysis of the continuous problem to reveal exact interface conditions which, after discretization, yield superior stability and accuracy properties. We generically term schemes built in this way as Added Mass Partitioned (AMP).
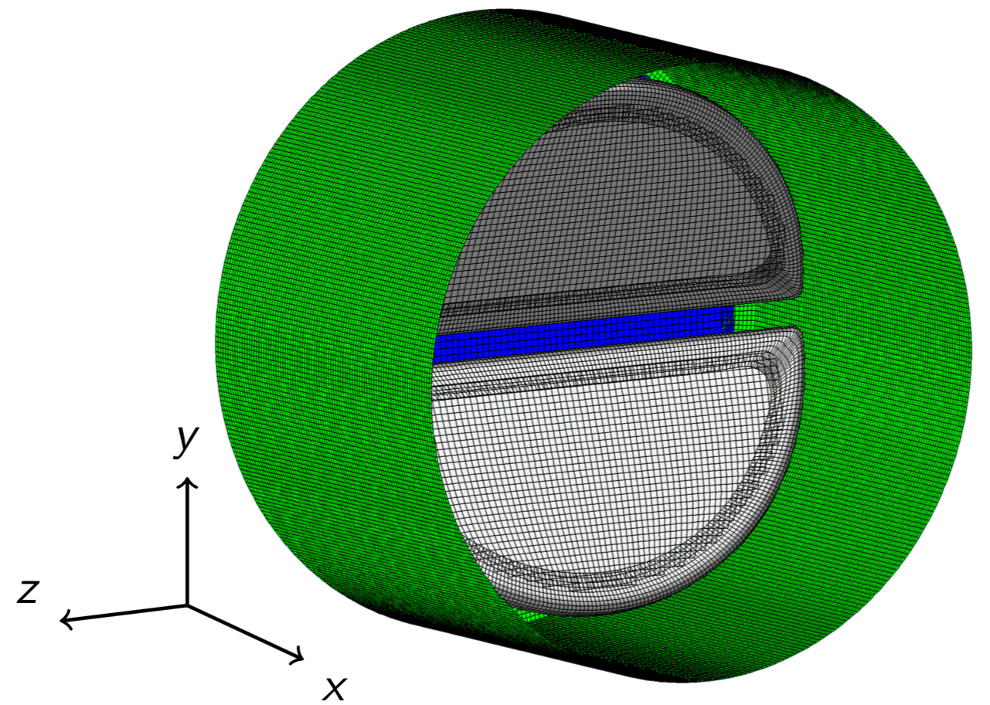
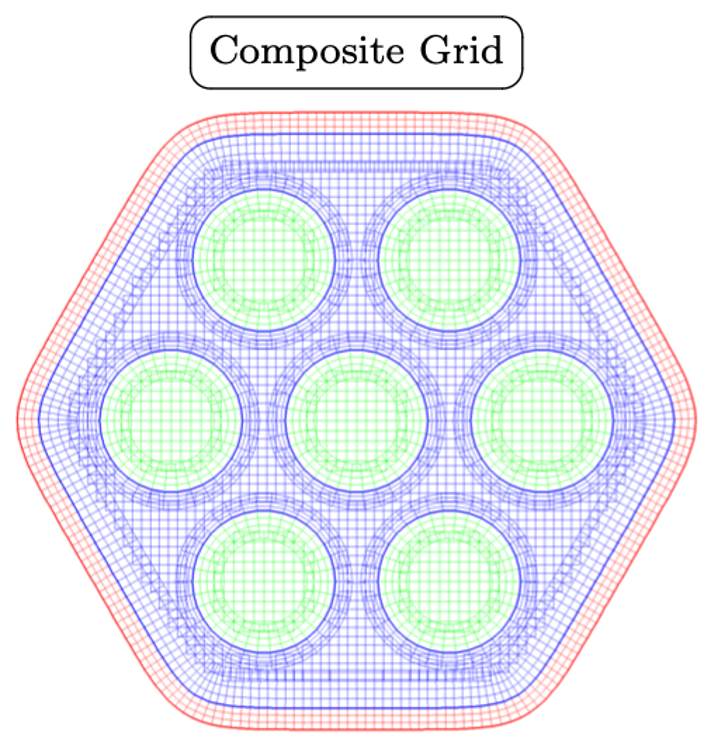
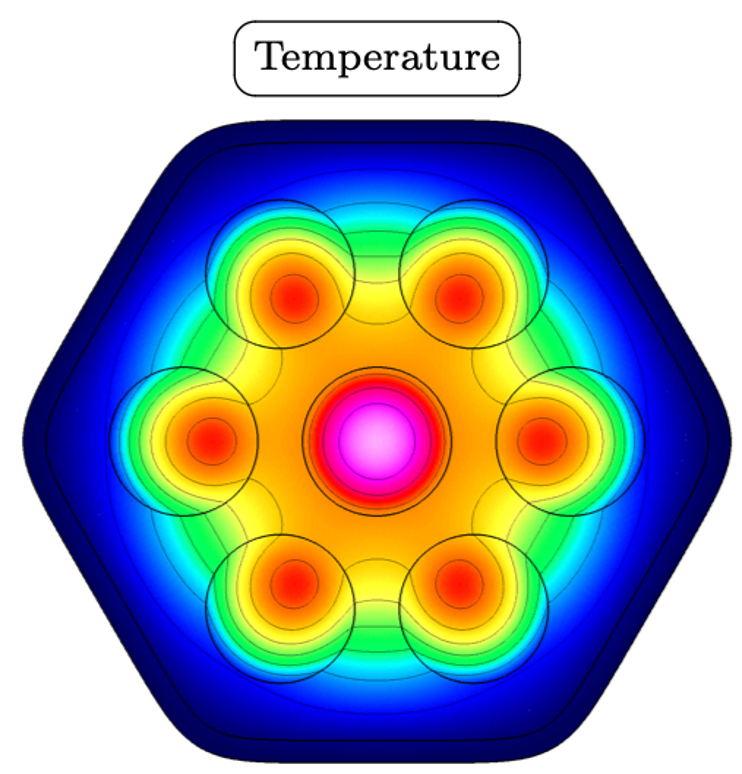
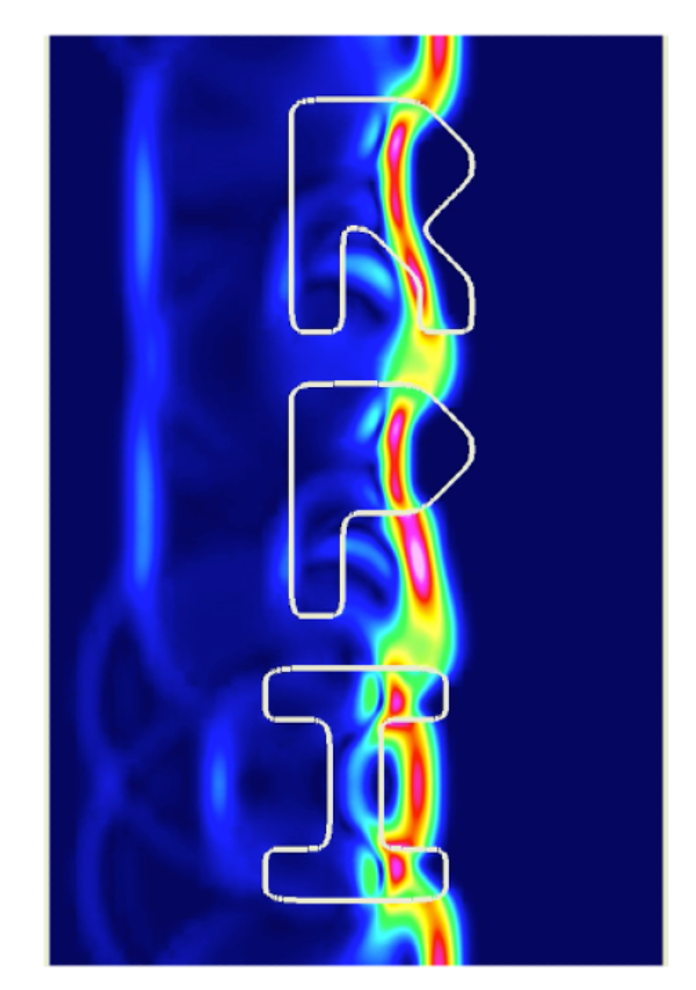
AMP scheme: Conjugate Heat Transfer (CHT)
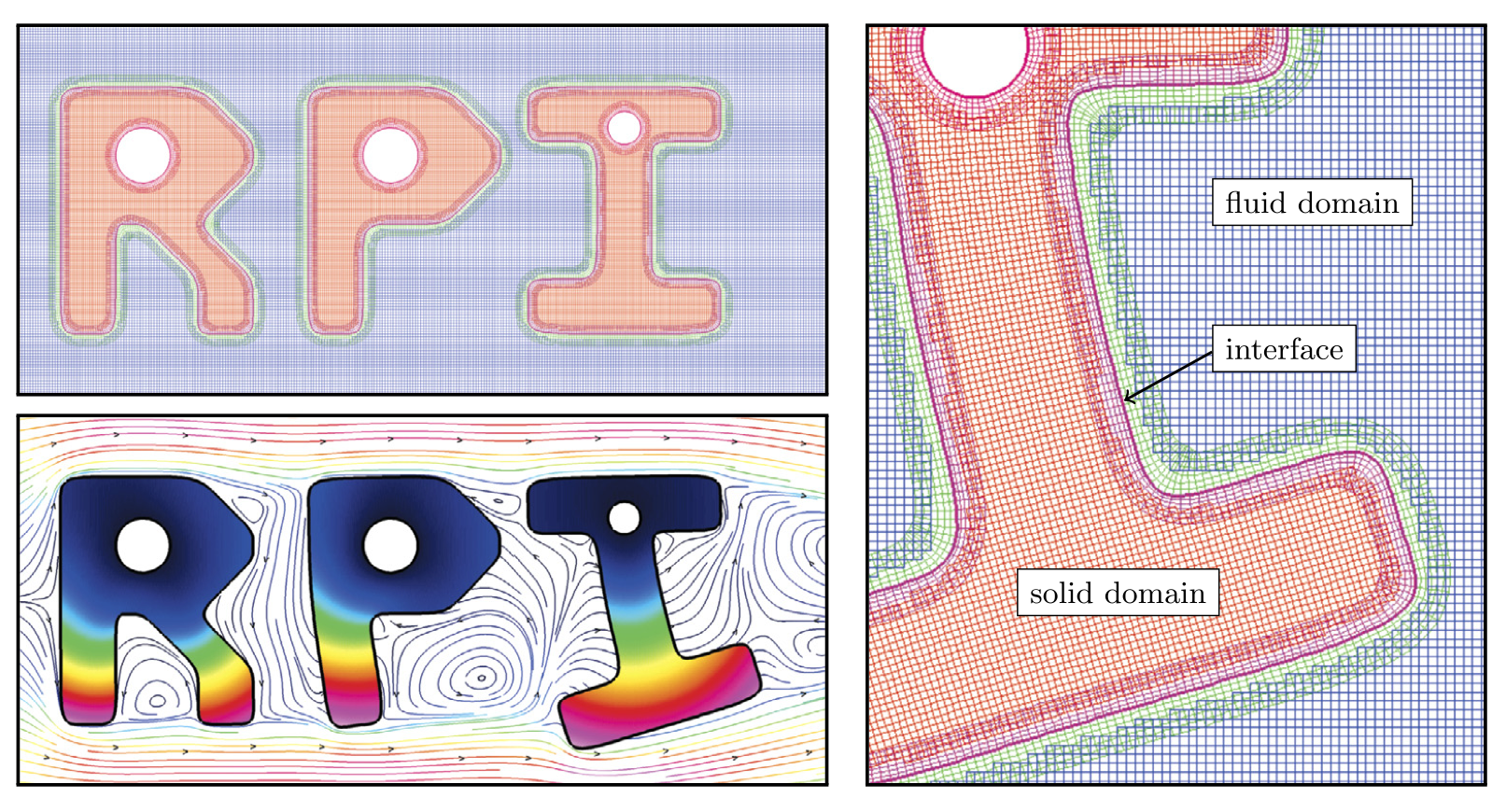
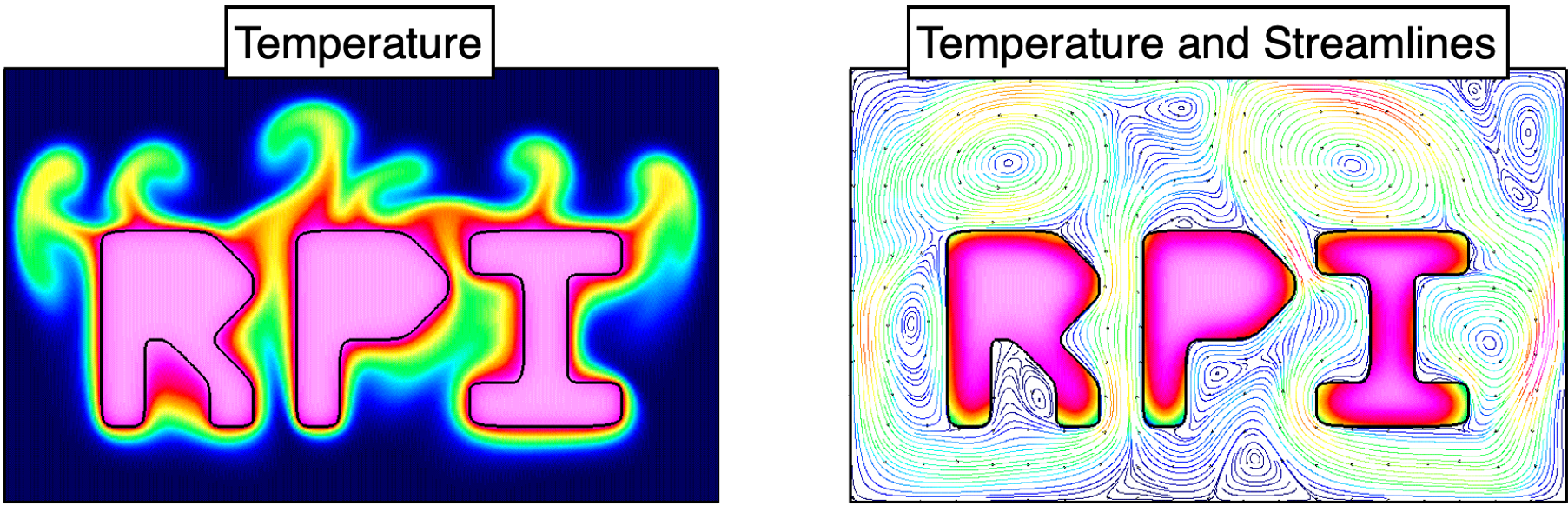
Similar coupling techniques are developed for other multi-domain problems. In the examples below we show just conjugate heat transfer in a mock reactor, in the middle we show fully coupled heat transfer and incompressible flow around heated letters RPI, and at bottom we show electromagnetic wave propagation through dispersive metals.
Discontinuous Galerkin Methods
High order discontinuous Galerkin methods are designed to preserve important structures and properties of PDE models. Examples include locally divergence-free methods for Maxwell equations, locally and globally divergence-free methods for ideal MHD equations, well-balanced methods for shallow-water equations, energy stable methods for Vlasolv-Maxwell equations and nonlinear optics models, and positivity-preserving methods for hyperbolic conservation laws.
- M. Lyu, V.A. Bokil, Y. Cheng, F. Li, Energy stable nodal discontinuous Galerkin methods for nonlinear Maxwell's equations in multi-dimensions, Journal of Scientific Computing, v89 (2021)
- Y. Cheng, I. Gamba, F. Li, P. Morrison, Discontinuous Galerkin methods for Vlasov-Maxwell equations, SIAM Journal on Numerical Analysis, v52-2 (2014), pp. 1017-1049
- F. Li and L. Xu, Arbitrary order exactly divergence-free central discontinuous Galerkin methods for ideal MHD equations, Journal of Computational Physics, v231 (2012), pp.2655-2675
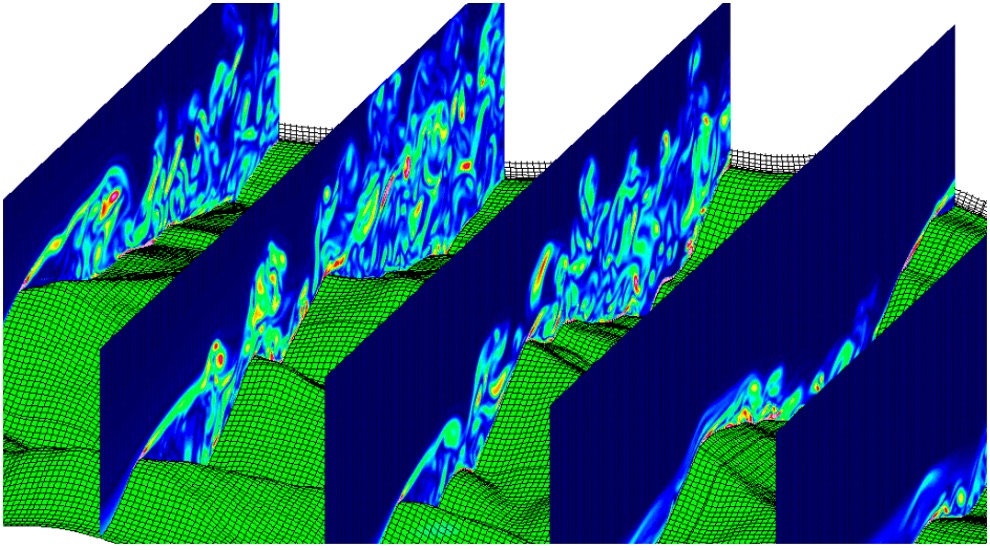
Asymptotic preserving methods for multi-scale kinetic transport simulation
Kinetic transport models, such as the radiative transfer equation and Boltzmann equation, are mesoscopic descriptions of the transport of particles such as neutrons and photons as well as their interactions with the background medium or among themselves. Such models are often multi-scale in nature. For example, radiative transfer equations can display both hyperbolic and diffusive characteristics depending on the strength of the scattering process. High order methods to simulate such models uniformly with respect to a broad range of regimes are designed and analyzed following the framework of asymptotic preserving methods that mimic the asymptotic behavior of the models at the discrete level. The main ingredients of the methods include model reformulations, suitable implicit-explicit time integrators, discrete ordinates angular discretization, and discontinuous Galerkin spatial discretization.

- K. Matsuda and F. Li, Multi-scale kinetic simulation: asymptotic preserving IMEX-BDF-DG schemes with three IMEX strategies, preprint (2024)
- Z. Peng and F. Li, Asymptotic preserving IMEX-DG-S schemes for linear kinetic transport equations based on Schur complement, SIAM Journal on Scientific Computing, v43 (2021), pp.A1194-A1220
- Z. Peng, Y. Cheng, J.-M. Qiu, F. Li, Stability-enhanced AP IMEX1-LDG method: energy-based stability and rigorous AP property, SIAM Journal on Numerical Analysis, v59 (2021), pp.925-954
- T. Xiong, J. Jang, F. Li, J.-M. Qiu, High order asymptotic preserving nodal discontinuous Galerkin IMEX schemes for the BGK equation, Journal of Computational Physics, v284 (2015), pp.70-94
Reduced order models for radiative transfer equations
One computational challenge shared by many kinetic transport models is the intrinsic high dimensionality, due to the unknown probability distribution functions defined on the phase space. Model order reduction strategies based on reduced basis methods are developed to mitigate the curse of dimensionality in simulating radiative transfer equations in certain regimes. They are also being designed to significantly reduce the computational complexity of solving the parametric radiative transfer equations and Boltzmann equation in multi-query settings, e.g., in optimal design and inverse problems.
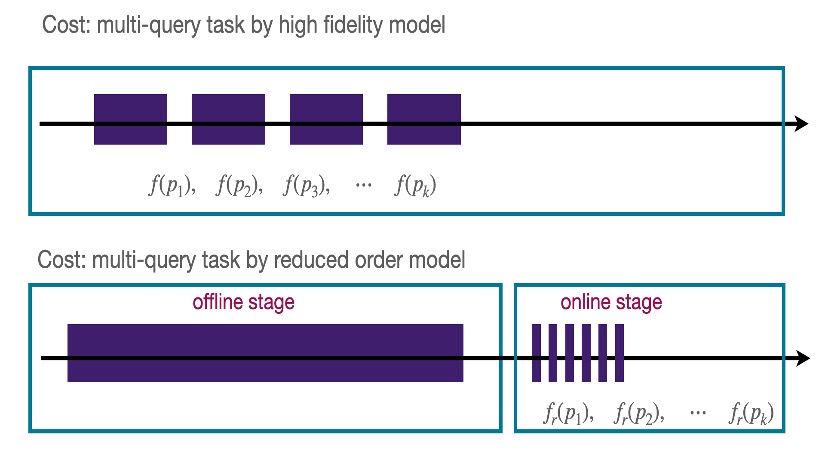
- Z. Peng, Y. Chen, Y. Cheng, F. Li, A micro-macro decomposed reduced basis method for the time-dependent radiative transfer equation, Multiscale Modeling & Simulation, v22 (2024), pp.639-666
- Z. Peng, Y. Chen, Y. Cheng, F. Li, A reduced basis method for radiative transfer equation, Journal of Scientific Computing, v91 (2022)