
Computational Biomechanics Current Research Topics:
High Performance Computing and Communications (HPCC) - Understanding Human Joint Mechanics Through Advanced Computational Models
This project is an interdisciplinary and inter-institutional five-year effort for the development of automated and adaptive three-dimensional (3-D) finite element analysis and parallel solution strategies to describe nonlinear moving contact problems characteristic of the biomechanics of joints in the human musculoskeletal system. Research methods involve the actual anatomic geometries and the multiphasic properties of the tissues in the joint.
Fundamental studies focus on:
- finite element 3D moving contact analysis of biphasic problems utilizing nonlinear hyperelastic finite deformation laws for tissue and non-Newtonian laws for the fluids;
- methods for the automatic and adaptive generation and control of 3D computational models using error estimates which take full account of the non-linearities, singularities, and boundary layer effects;
- integration of digitally measured anatomic data with the automated adaptive 3D mesh generation, and numerical methods for processing the material and geometric data required for the contact analysis;
- parallel solution algorithms for the nonlinear time-dependent problems utilizing state-of-the-art high-performance computer architectures; and
- correlation of computed predictions with experimental data for finite deformation material tests.
These essential developments will provide, for the first time, the sophisticated high-performance computational tools needed to make significant advances toward precise 3D simulations of biomechanical problems related to diarthrodial joints, with realistic loading conditions, joint geometries, and constituent material properties. These studies will advance the state of the art in reliable high-performance parallel and adaptive computational techniques and finite element formulations for nonlinear and moving contact problems in mechanics including those modeled as mixtures (for example, soft tissues and soils). They also will contribute significantly to an understanding of the complex biomechanical behaviors of normal and pathological human joints, and provide an essential component in the development of new clinical treatment modalities.
Solid modeling of physiological geometries
Soft tissues, such as cartilage and ligaments, play an important role in the function of the human musculoskeleton. In order to analyze these components, meshes of the corresponding anatomical regions have to be created. To create the meshes, 3D measurements have to be taken and geometric models created, augmented with additional information (such as loading and muscle forces), and passed to the meshing stage. These geometric models can be explicitly defined using current solid modeling engines such as Parasolid or by discrete implicit representations. Researchers are collaborating with the Orthopedic Research Laboratory at Columbia University.

Contact analysis of biphasic tissues
Researchers' primary interest is in the response of articular cartilage to the loads imposed by articulating a joint. The biphasic theory is being used to provide the mathematical description of this response. That theory models soft tissues as a binary mixture of an incompressible, elastic solid and an incompressible, inviscid fluid. Boundary conditions for interfaces between biphasic materials are written for a surface between two domains. Researchers assume frictionless contact and arrive at four contact continuity relations: continuity of pressure, normal component of elastic solid traction, normal solid velocity, and normal relative fluid flow. (Note that fluid velocity is not required to be continuous for biphasic continua in contact.)
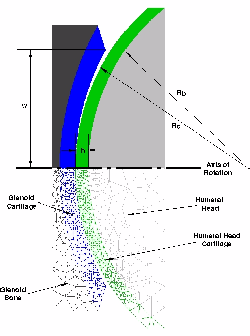
The diagram represents the geometric description of an axisymmetric model of the gleno-humeral joint of the shoulder; the finite element mesh is given in the lower portion of the figure. Both the glenoid and humeral head cartilage are treated as transversely isotropic with stiffening fibers tangent to the tissue surface. Click to enlarge.
Researchers use the Galerkin weighted residual method to generate finite element equations. For the contact problem, a weighted residual is constructed from the governing differential equations, the traction boundary conditions and the four contact conditions. Drawing analogies from variational finite element formulations, two new variables are defined and introduced into the weighted residual. This both enforces traction continuity and produces symmetric matrix equations.
Nonlinear continuum mixture theories
Due to the complex geometry of diarthrodial joints like the knee and the shoulder, physiological problems in joint biomechanics are essentially 3D. Even when the mechanical behavior of a single component is analyzed (the layer of articular cartilage, for instance) it is difficult to circumvent this fact because the size and shape of physiological cartilage layers limit the use of plane strain models, and the fact that many load conditions are poorly represented by axisymmetric models. Articular cartilage can be represented as a highly nonlinear biphasic material, consisting of an incompressible solid phase (collagen and proteoglycan) and an incompressible inviscid fluid phase (interstitial water).
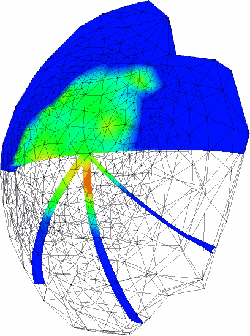
This is an image of the pressure in the humeral head cartilage after one second of creep loading. The load is distributed across the surface based on geometric information of the glenoid position relative to the humeral head, and is scaled and shared between the solid and fluid phases based on results from 2-D contact simulations. Observe that there are gradients through the tissue thickness.
To address these complex 3D problems, researchers developed a 3D mixed-penalty finite element using the Galerkin weighted residual method. Geometric and material non-linearities were included, the latter in the form of a nonlinear hyperelastic constitutive law and a strain-dependent permeability law. Because of the incompressibility condition, a 20-node hexahedron with tri-quadratic functions was used for the interpolation of solid and fluid phase kinematic fields and a linear function for the interpolation of the pressure field. The governing equations correspond to the biphasic theory for soft hydrated tissues developed by Mow, et. al. The resulting finite element equations constitute a system of nonlinear first order differential equations in the fluid and solid phase velocities.
